 |
(1) Knowns = R, S, where:
|
OTCUTS©
OTCUTS© is a computer spreadsheet program (a href="otcuts.zip">copy of which is free) designed to calculate the parameters needed to design and execute an ornamental turned cutting pattern on a cylindrical surface with a vertical cutting frame, typically known as a basketwork-type cutting pattern. This cutting pattern may typically be set up by a trial-and-error method by bringing the cutter into the workpiece incrementally until the ‘corners’ or points of the cut are sharp and the cutter has just cut below the original surface of the workpiece at the high points of the cut. The advantage of this technique of calculation over the trial-and-error method is that a table may be quickly generated which will give the cut sizes, both in length and depth, for all the number of divisions on the index plate at once. This then allows the turner to visualize, based on the width of the cutter, how coarse or fine a pattern may appear on the piece and so be an aid in the design of the piece before any actual cuts are ever made. By so relating the width of the cutter to its cutting depth and length of cut, a feeling may be gained for the final aesthetics of the design. For example, a smaller number of cuts will make for a deeper cut which will produce a stronger contrast in the surface pattern, and a more forceful effect in the final piece. On the contrary, a greater number of cuts at a shallower depth will make the pattern more subtle and have a less prominent impact on the overall design. Also, one may choose a number of cuts for an intended relation between the width of cutter and length of cut; for example, using the Golden Mean proportion of 1.618…
The following information describes the OTCUTS system:
(1) The mathematical derivation of the formulas used to calculate the necessary OT parameters, including a diagram with the relevant abbreviations for all parameters used.
(2) TABLE I—a chart of the number of division plate holes to move to divide the workpiece using only these marked holes to avoid confusion: 3-4-6-8-9-12. By setting up your index plate with hole circles of 192-144-120-108-96-84 such as I have done, all regular divisions of the workpiece can be obtained by moving the index pin into these marked holes which have color-coded dots
(3) TABLE II—The calculation spreadsheet itself with a list of the formulas to calculate each column. This reproduction is just an arbitrary sample calculation to illustrate how the table filled with the data fields looks. I have left all the intermediate calculations in the spreadsheet for clarity to illustrate all of the variable calculations necessary to arrive at the final depth of cut.
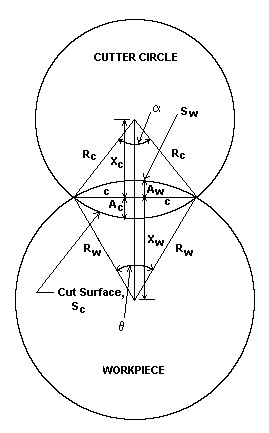
In use, one needs only to enter into TABLE II the variables Rw, which is the radius of the workpiece surface to be ornamented, and Rc, which is the radius of the cutting arc measured from the axis of the cutting frame spindle to the tip of the cutting edge, on the row for N = 2 and all the rest of the calculations will be performed by the built-in spreadsheet formulas. Sw is the arc of the workpiece which is subtended by the chord, 2c, drawn between two adjacent high points of the cut. Sc is the actual length of the finished cut left by the cutter on the workpiece between two adjacent high points of the cut. Aw is the distance from the original workpiece surface to chord 2c which would represent the flat of a polygon of ‘N’ sides. Ac is the distance below chord 2c to the bottom of the finished arc cut by the cutter and would be the depth that the finished pattern would be below a polygon of ‘N’ sides. Finally, At is the total depth to set the cutter below the initial cylindrical surface of the workpiece to make the high point of the cut sharp and crisp. In practice, one might cut a few thousandths deeper to compensate for any errors in measurement or out-of-roundness in mounting the workpiece in the lathe. The diagram on the formula derivation page graphically depicts these various parameters. It should be apparent how these data would help to compare designs using differing numbers of divisions of the workpiece and cutter widths to arrive at pleasing proportions for the piece.
If, on entering particular values for Rw and Rc , an error message appears on any of the calculated cells of the spreadsheet, these particular combinations of N, Rw and Rc are not possible. This program was prepared on a Microsoft Excel 97 spreadsheet for an IBM-PCand can be converted to other common spreadsheet formats. The spreadsheet file has been zipped to decrease download time and is available for individual use from the download link below.
• Download OTCUTS©
Mathematical Derivations
 |
(1) Knowns = R, S, where:
|
DERIVATIONS OF FORMULAS USED IN SPREADSHEET
1. Find Aw:
a. From GENERAL FORMULAS (GF) (1) (b), * Sw = (2
pRw)/N *b. From GF (3),
q = Sw/Rw = [(2pRw)/N]/Rw = (2p)/Nc.
\ q/2 = p/N, and from cos (q/2) = Xw/Rw, then Xw = Rwcos(p/N)d. From GF (4), Aw = Rw - Xw = Rw - Rwcos(
p/N), so * Aw = Rw[1 - cos(p/N)] *2. Find c:
a. sin (
q/2) = c/Rw, \ c = Rwsin(p/N) and * 2c = 2Rwsin(p/N) *3. Find
a:a. sin (
a/2) = c/Rc = [Rwsin(p/N)]/ Rc, \ * a/2 = sin-1[(Rw/Rc)sin(p/N)] *4. Find Ac:
a. cos (a/2) = Xc /Rc, \ Xc = Rc cos (a/2)
b. From GF (4), Ac = Rc - Xc = Rc - Rc cos (a/2), so * Ac = Rc[1 - cos (a/2)] *
5. So, from GF (9), * At = Rw[1 - cos(p/N)] + Rc[1 - cos (a/2)] *
TABLE I – Index Plate Divisions to Move to Place Index Only in Marked Holes (3-4-6-8-9-12)
DIVISIONS= |
INDEX PLATE HOLE CIRCLES |
|||||
N |
84 |
96 |
108 |
120 |
144 |
192 |
2 |
~ |
48 |
~ |
~ |
72 |
96 |
3 |
~ |
~ |
~ |
~ |
48 |
~ |
4 |
~ |
24 |
~ |
~ |
~ |
48 |
5 |
~ |
~ |
~ |
24 |
~ |
~ |
6 |
~ |
~ |
~ |
~ |
24 |
~ |
7 |
12 |
~ |
~ |
~ |
~ |
~ |
8 |
~ |
12 |
~ |
~ |
~ |
24 |
9 |
~ |
~ |
12 |
~ |
~ |
~ |
10 |
~ |
~ |
~ |
12 |
~ |
~ |
12 |
~ |
~ |
~ |
~ |
12 |
~ |
14 |
6 |
~ |
~ |
~ |
~ |
~ |
15 |
~ |
~ |
~ |
8 |
~ |
~ |
16 |
~ |
6 |
~ |
~ |
~ |
12 |
18 |
~ |
~ |
6 |
~ |
~ |
~ |
20 |
~ |
~ |
~ |
6 |
~ |
~ |
21 |
4 |
~ |
~ |
~ |
~ |
~ |
24 |
~ |
~ |
~ |
~ |
6 |
8 |
27 |
~ |
~ |
4 |
~ |
~ |
~ |
28 |
3 |
~ |
~ |
~ |
~ |
~ |
30 |
~ |
~ |
~ |
4 |
~ |
~ |
32 |
~ |
3 |
~ |
~ |
~ |
6 |
36 |
~ |
~ |
3 |
~ |
4 |
~ |
40 |
~ |
~ |
~ |
3 |
~ |
~ |
42 |
2 |
~ |
~ |
~ |
~ |
~ |
48 |
~ |
2 |
~ |
~ |
~ |
4 |
54 |
~ |
~ |
2 |
~ |
~ |
~ |
60 |
~ |
~ |
~ |
2 |
~ |
~ |
64 |
~ |
~ |
~ |
~ |
~ |
3 |
72 |
~ |
~ |
~ |
~ |
2 |
~ |
84 |
1 |
~ |
~ |
~ |
~ |
~ |
96 |
~ |
1 |
~ |
~ |
~ |
2 |
108 |
~ |
~ |
1 |
~ |
~ |
~ |
120 |
~ |
~ |
~ |
1 |
~ |
~ |
144 |
~ |
~ |
~ |
~ |
1 |
~ |
192 |
~ |
~ |
~ |
~ |
~ |
1 |
TABLE II – A Sample Spreadsheet
SUMMARY OF FORMULAS USED IN CALCULATIONS:
Sw = (2p/N)Rw = Arc of workpiece surface between points of cut.
2c = 2Rwsin(p/N) = Length of chord between points of cut.
Sc = Rca = 2Rcsin-1[(Rw/Rc)sin(p/N)] = Cut surface, actual length of arc
formed by cutter on workpiece between points of cut.
Aw = Rw[1 -
cos(p/N)] = Depth of cut from
workpiece surface to chord '2c'.
a/2 = sin-1[(Rw/Rc)sin(p/N)] = 1/2 external angle formed by
intersection of tangents to workpiece at points of cuts.
Ac = Rc[1 -
cos(a/2)] = Depth of cut from
chord '2c' to bottom of cut surface on workpiece.
At = Aw + Ac
= Total depth of cut from workpiece surface to bottom of cut surface.
Where N = Number of cuts, Rw
= radius of workpiece, & Rc = radius of cutter's cutting arc.
Angle in radians; for degrees, multiply by 180/p. All
dimensions = 0.00000".
N |
R w |
R c |
S w |
2c |
S c |
A w |
a /2(RAD.) |
A c |
A t |
2 |
0.94750 |
1.30000 |
2.97666 |
1.89500 |
2.12325 |
0.94750 |
0.81664 |
0.40992 |
1.35742 |
3 |
0.94750 |
1.30000 |
1.98444 |
1.64112 |
1.77606 |
0.47375 |
0.68310 |
0.29169 |
0.76544 |
4 |
0.94750 |
1.30000 |
1.48833 |
1.33997 |
1.40775 |
0.27752 |
0.54144 |
0.18594 |
0.46346 |
5 |
0.94750 |
1.30000 |
1.19066 |
1.11385 |
1.15109 |
0.18096 |
0.44273 |
0.12534 |
0.30629 |
6 |
0.94750 |
1.30000 |
0.99222 |
0.94750 |
0.96983 |
0.12694 |
0.37301 |
0.08940 |
0.21634 |
7 |
0.94750 |
1.30000 |
0.85047 |
0.82221 |
0.83657 |
0.09383 |
0.32176 |
0.06671 |
0.16055 |
8 |
0.94750 |
1.30000 |
0.74416 |
0.72519 |
0.73493 |
0.07212 |
0.28267 |
0.05159 |
0.12371 |
9 |
0.94750 |
1.30000 |
0.66148 |
0.64813 |
0.65504 |
0.05714 |
0.25194 |
0.04104 |
0.09818 |
10 |
0.94750 |
1.30000 |
0.59533 |
0.58559 |
0.59065 |
0.04637 |
0.22717 |
0.03340 |
0.07978 |
12 |
0.94750 |
1.30000 |
0.49611 |
0.49046 |
0.49342 |
0.03229 |
0.18978 |
0.02334 |
0.05562 |
14 |
0.94750 |
1.30000 |
0.42524 |
0.42168 |
0.42355 |
0.02376 |
0.16290 |
0.01721 |
0.04097 |
15 |
0.94750 |
1.30000 |
0.39689 |
0.39399 |
0.39552 |
0.02071 |
0.15212 |
0.01501 |
0.03572 |
16 |
0.94750 |
1.30000 |
0.37208 |
0.36970 |
0.37095 |
0.01821 |
0.14267 |
0.01321 |
0.03141 |
18 |
0.94750 |
1.30000 |
0.33074 |
0.32906 |
0.32995 |
0.01439 |
0.12690 |
0.01045 |
0.02485 |
20 |
0.94750 |
1.30000 |
0.29767 |
0.29644 |
0.29709 |
0.01167 |
0.11427 |
0.00848 |
0.02014 |
21 |
0.94750 |
1.30000 |
0.28349 |
0.28244 |
0.28299 |
0.01058 |
0.10884 |
0.00769 |
0.01828 |
24 |
0.94750 |
1.30000 |
0.24805 |
0.24735 |
0.24772 |
0.00811 |
0.09528 |
0.00590 |
0.01400 |
27 |
0.94750 |
1.30000 |
0.22049 |
0.22000 |
0.22026 |
0.00641 |
0.08472 |
0.00466 |
0.01107 |
28 |
0.94750 |
1.30000 |
0.21262 |
0.21217 |
0.21241 |
0.00596 |
0.08170 |
0.00434 |
0.01029 |
30 |
0.94750 |
1.30000 |
0.19844 |
0.19808 |
0.19827 |
0.00519 |
0.07626 |
0.00378 |
0.00897 |
32 |
0.94750 |
1.30000 |
0.18604 |
0.18574 |
0.18590 |
0.00456 |
0.07150 |
0.00332 |
0.00788 |
36 |
0.94750 |
1.30000 |
0.16537 |
0.16516 |
0.16527 |
0.00361 |
0.06357 |
0.00263 |
0.00623 |
40 |
0.94750 |
1.30000 |
0.14883 |
0.14868 |
0.14876 |
0.00292 |
0.05722 |
0.00213 |
0.00505 |
42 |
0.94750 |
1.30000 |
0.14175 |
0.14161 |
0.14168 |
0.00265 |
0.05449 |
0.00193 |
0.00458 |
48 |
0.94750 |
1.30000 |
0.12403 |
0.12394 |
0.12399 |
0.00203 |
0.04769 |
0.00148 |
0.00351 |
54 |
0.94750 |
1.30000 |
0.11025 |
0.11018 |
0.11022 |
0.00160 |
0.04239 |
0.00117 |
0.00277 |
60 |
0.94750 |
1.30000 |
0.09922 |
0.09918 |
0.09920 |
0.00130 |
0.03815 |
0.00095 |
0.00224 |
64 |
0.94750 |
1.30000 |
0.09302 |
0.09298 |
0.09300 |
0.00114 |
0.03577 |
0.00083 |
0.00197 |
72 |
0.94750 |
1.30000 |
0.08268 |
0.08266 |
0.08267 |
0.00090 |
0.03180 |
0.00066 |
0.00156 |
84 |
0.94750 |
1.30000 |
0.07087 |
0.07086 |
0.07087 |
0.00066 |
0.02726 |
0.00048 |
0.00115 |
96 |
0.94750 |
1.30000 |
0.06201 |
0.06200 |
0.06201 |
0.00051 |
0.02385 |
0.00037 |
0.00088 |
108 |
0.94750 |
1.30000 |
0.05512 |
0.05512 |
0.05512 |
0.00040 |
0.02120 |
0.00029 |
0.00069 |
120 |
0.94750 |
1.30000 |
0.04961 |
0.04961 |
0.04961 |
0.00032 |
0.01908 |
0.00024 |
0.00056 |
144 |
0.94750 |
1.30000 |
0.04134 |
0.04134 |
0.04134 |
0.00023 |
0.01590 |
0.00016 |
0.00039 |
192 |
0.94750 |
1.30000 |
0.03101 |
0.03101 |
0.03101 |
0.00013 |
0.01193 |
0.00009 |
0.00022 |
World-Wide Web presentation Copyright © 1996, James E. Harris. All Rights Reserved.
Last revised 18 September, 1999.